



suivant: À propos de ce
monter: L'effet papillon
précédent: Bibliographie
Table des matières
Sous-sections
Toutes les procédures présentées ont été réalisées sous MAPPLE .
A chaque fois elles servent à étudier une suite de type :
Comme nous voulons étudier le comportement de la suite en fonction de  , on va essayer de représenter son comportement au voisinage
de l'infini en fonction de
, on va essayer de représenter son comportement au voisinage
de l'infini en fonction de  . On met donc en place un graphique à deux dimensions, où figureront en abscisses les valeurs de
. On met donc en place un graphique à deux dimensions, où figureront en abscisses les valeurs de  et en
ordonnées les valeurs de la suite au voisinage de l'infini.
et en
ordonnées les valeurs de la suite au voisinage de l'infini.
![$[Amin;Amax]$](img78.png) réprésente l'intervalle de variation de
réprésente l'intervalle de variation de  ,
,
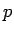 réprésente le pas utilisé,
réprésente le pas utilisé,
 correspond à la valeur de
correspond à la valeur de  à partir de laquelle on commence à afficher les points,
à partir de laquelle on commence à afficher les points,
 correspond à la valeur de
correspond à la valeur de  pour laquelle on stoppe les calculs.
pour laquelle on stoppe les calculs.
bifurc:=proc(Amin,Amax,p,Nmin,Nmax);
M:=NULL;
g:=x->(x*(1-x));
for a from Amin to Amax by p do
L:=NULL;
t:=0.4;
for k from 1 to Nmin do t:=a*evalf(g(t)) od;
for k from Nmin to Nmax do
L:=L,[a,t];
t:=evalf(a*g(t));
od;
M:=M,plot([L],x=Amin..Amax,style=point,symbol=point);
od;
display([M]);
end:
Il s'agit de réprésenter la fonction  qui définit la suite, ainsi que la droite d'équation
qui définit la suite, ainsi que la droite d'équation  , puis de montrer comment se définit
, puis de montrer comment se définit
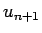 en fonction de
en fonction de  .
.
 est la fonction à partir de laquelle les calculs sont effectués,
est la fonction à partir de laquelle les calculs sont effectués,
 est le nombre d'itérations que l'on désire afficher,
est le nombre d'itérations que l'on désire afficher,
 est la valeur initiale de la suite.
est la valeur initiale de la suite.
suite:=proc(f,n,u0);
L:=[u0,0];
t:=u0;
for k from 1 to n do
L:=L,[t,t],[t,f(t)];
t:=f(t);
od;
plot([x,f(x),[L]],x=0..1,color=[black,red,blue]);
end:
On cherche ici à illustrer le phénomène de sensibilité aux conditions initiales. On prend donc deux suites ne différant que par leur terme
initial. Puis on représente les itérés de l'une en fonction des itérés de l'autre.
 : fonction qui définit les deux suites,
: fonction qui définit les deux suites,
 : terme initial de la première suite,
: terme initial de la première suite,
 : terme inital de la seconde suite,
: terme inital de la seconde suite,
 : nombre d'itérations à représenter.
: nombre d'itérations à représenter.
pap:=proc(f,u0,v0,n);
L:=[u0,v0];
x:=u0;
y:=v0;
for k from 1 to n do
x:=f(x);
y:=f(y);
L:=L,[x,y];
od;
plot([L],style=point);
end:
On utilise le même système de représentation que dans le cas précédent pour illustrer les erreurs d'arrondi que peut commettre
l'ordinateur. Ici le terme initial est le même pour les deux suites, mais c'est l'expression de  qui diffère, on prendra par exemple
qui diffère, on prendra par exemple  factorisée puis développée.
factorisée puis développée.
 et
et  : les fonctions définissant les deux suites,
: les fonctions définissant les deux suites,
 : le terme initial pour chaque suite,
: le terme initial pour chaque suite,
 : le nombre d'itérations à représenter.
: le nombre d'itérations à représenter.
pap2:=proc(f,g,u0,n);
L:=[u0,u0];
x:=u0;
y:=u0;
for k from 1 to n do
x:=f(x);
y:=g(y);
L:=L,[x,y];
od;
plot([L],style=point);
end:




suivant: À propos de ce
monter: L'effet papillon
précédent: Bibliographie
Table des matières
Sébastien Georget
2003-09-18
![\begin{displaymath}
\left \{
\begin{array}{ccc}
u_0 &\in& [0;1]\\
u_{n+1} &=& f(u_n)
\end{array}
\right.
\end{displaymath}](img3.png)
![\begin{displaymath}
\left \{
\begin{array}{ccc}
u_0 &\in& [0;1]\\
u_{n+1} &=& f(u_n)
\end{array}
\right.
\end{displaymath}](img3.png)