L'effet papillon
Georget Sébastien
29 avril 2000
L'expression "effet papillon" a été la première fois utilisée par Edward Lorenz. Celui ci l'employa pour décrire un phénomène
connu en mathématiques sous le nom de sensibilité aux conditions initiales. Phénomène qu'il mit en évidence grâce au système d'équations
différentielles suivant :
Système qu'il obtint en simplifiant à l'extrème un modèle de convection thermique. Celui-ci a pour particularité d'être non linéaire et
c'est ce qui le rend impossible à résoudre par les méthodes usuelles.
Nous allons ici nous intéresser à un système plus simple que celui de Lorenz, mais qui présente cependant des comportements
semblables du eux-mêmes à des non-linéarités du système. Il s'agit de la suite logistique.
Comme le système différentiel présenté plus haut, cette suite est issue d'une modélisation d'un phnomène naturel : l'évolution des effectifs
d'une population de type proies-prédateurs dan un système clot.
Plus précisemment, le modèle conduit à une équation différentielle que l'on peut par des méthodes de discrétisation ramener à une suite
récurrente.
Nous allons procéder à l'étude de cette suite en suivant son évolution d'un comportement simple (la convergence) vers un comportement plus
complexe (le chaos) en passant par un état intermédiaire (la périodicité).
Dans cette section, nous allons définir ce qu'est la suite logistique puis nous verrons une méthode pratique permettant de la construire et
de l'étudier.
La suite logistique est définie ainsi :
où la fonction  est une fonction paramétrée définie de la manière suivante :
est une fonction paramétrée définie de la manière suivante :
On prendra par la suite ![$a \in [0;4]$](img6.png) de manière à ce que l'intervalle
de manière à ce que l'intervalle ![$[0;1]$](img7.png) soit stable par
soit stable par  .
.
Pour visualiser une telle suite il existe une représentation utile que l'on appelle la représentation en toile d'araignée. Nous allons
voir avec un exemple comment elle fonctionne.
Puisque 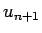 est déterminé à partir de
est déterminé à partir de  , on trace la droite d'équation
, on trace la droite d'équation  , puis à chaque itération, on reporte la
valeurde
, puis à chaque itération, on reporte la
valeurde  sur cette droite et on en recherche l'image par
sur cette droite et on en recherche l'image par  .
.
Sur l'exemple précédent, nous avons vu que la suite convergeait vers un point fixe. On peut se demander si se comportement est valable
pour toutes les valeurs de ![$a \in [0;4]$](img6.png) . Pour voir rapidement ce qu'il en est nous allons utiliser le diagramme de bifurcation.
. Pour voir rapidement ce qu'il en est nous allons utiliser le diagramme de bifurcation.
Comme nous voulons étudier le comportement de la suite en fonction de  , on va essayer de représenter son comportement au voisinage
de l'infini en fonction de
, on va essayer de représenter son comportement au voisinage
de l'infini en fonction de  . On met donc en place un graphique à deux dimensions, où figureront en abscisses les valeurs de
. On met donc en place un graphique à deux dimensions, où figureront en abscisses les valeurs de  et en
ordonnées les valeurs de la suite au voisinage de l'infini.
et en
ordonnées les valeurs de la suite au voisinage de l'infini.
On supposera en fait que le comportement de la suite se stabilise très vite. Ce qui nous permettra d'étudier la suite à partir d'un
rang  accessible aux capacités de l'ordinateur. Ensuite nous représenterons les éléments de la suites pour
accessible aux capacités de l'ordinateur. Ensuite nous représenterons les éléments de la suites pour  variant de
variant de  à
à
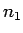 , en prenant
, en prenant 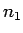 suffisament grand pour qu'on soit quasiment sur du comportement de la suite, mais pas trop grand afin de conservé
des temps de calcul raisonnables.
suffisament grand pour qu'on soit quasiment sur du comportement de la suite, mais pas trop grand afin de conservé
des temps de calcul raisonnables.
Ici, nous avons choisi  et
et  .
.
Nous obtenons grâce à la procédure bifurc (voir page ![[*]](crossref.png) ), le diagramme de bifurcation suivant, aussi appelé
diagramme de FeigenBaum.
), le diagramme de bifurcation suivant, aussi appelé
diagramme de FeigenBaum.
On peut tout de suite voir que la suite ne présente pas toujours un comportement aussi simple que celui que nous avons vu
précédemment. En effet, il semble qu'il existe des valeurs de  à partir desquelles le diagramme se divise en deux. Ce qui se traduit au
niveau de la suite par l'apparition de cycles.
à partir desquelles le diagramme se divise en deux. Ce qui se traduit au
niveau de la suite par l'apparition de cycles.
Tout d'abord, nous allons nous limiter à l'étude de la première bifurcation. C'est à dire que nous allons chercher pour quelle valeur
de  la suite ne converge plus. Mais pour cela, nous devons essayer de comprendre pourquoi la convergence disparaît, c'est ce que nous
allons voir.
la suite ne converge plus. Mais pour cela, nous devons essayer de comprendre pourquoi la convergence disparaît, c'est ce que nous
allons voir.
En fait, la représentation en toile d'araignée va nous permettre de comprendre ce qui se passe.
Etudions localement comment se comporte la suite dans le domaine de convergence (par exemple  ) et dans le domaine où
elle ne converge plus (par exemple
) et dans le domaine où
elle ne converge plus (par exemple  ).
Rerprésentons en plus sur les schémas la tangente au point d'intersection
).
Rerprésentons en plus sur les schémas la tangente au point d'intersection  entre la courbe représentative de
entre la courbe représentative de  et la première
bissectrice du repère.
et la première
bissectrice du repère.
Graphiquement, on comprend bien pourquoi la suite va cesser de converger.
En effet, tant que le coefficient directeur de la tangente en  est supérieur à
est supérieur à  , localement chaque itéré se rapproche du point
fixe. Dans ce cas, le point fixe est un point attractif (ou stable). Mais dès qu'il est inférieur à
, localement chaque itéré se rapproche du point
fixe. Dans ce cas, le point fixe est un point attractif (ou stable). Mais dès qu'il est inférieur à  , les itérés auront tendance à s'en
écarter. On dit alors que le point devient répulsif (ou instable).
, les itérés auront tendance à s'en
écarter. On dit alors que le point devient répulsif (ou instable).
Pour trouver la valeur de  à partir de laquelle la suite ne converge plus,
il faut donc trouver quand le coefficient de la tangente au point fixe passe par
à partir de laquelle la suite ne converge plus,
il faut donc trouver quand le coefficient de la tangente au point fixe passe par  .
.
Nous devons donc, dans un premier temps, résoudre l'équation  afin de déterminer le point fixe. On obient
afin de déterminer le point fixe. On obient
 .
.
Il nous faut ensuite déterminer la dérivée en ce point : 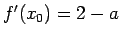 .
.
On trouve donc que la suite cesse de converger lorsque  , ce qu'on pouvait deviner sur le graphique.
, ce qu'on pouvait deviner sur le graphique.
On pourrait poursuive et déterminer ainsi les points de bifurcation suivants. Cependant les calculs deviennent rapidement très lourds,
puisque pour déterminer le point de 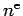 bifurcation, il faut résoudre l'équation
bifurcation, il faut résoudre l'équation  , c'est à dire un polynôme de degré
, c'est à dire un polynôme de degré  . On
n'obtiendra donc que des valeurs approchées.
. On
n'obtiendra donc que des valeurs approchées.
A titre d'exemple voici les deux points de bifurcation suivants.
Cet exemple, laisse supposer que pour chaque nouvelle branche définie, la bifurcation suivante aura lieu en même temps que sur les
autres branches.
Nous allons commencer par définir mathématiquement un cycle, puis nous verrons un théorème important pour l'étude de la suite logistique.
On définit un n-cycle ou cycle d'ordre n de la manière suivant :
avec :
A partir du diagramme de Feigenbaum, on peut penser que les cycles vont apparaîtres dans l'ordre des puissances de  .
.
C'est effectivement le cas, mais grâce à un mathématicien russe : A.N. Sharkovski, on sait depuis 1964 que ce ne sont pas les
seuls. Il a même démontré dans quels ordre apparaîssent les cycles. C'est ce que nous allons voir maintenant.
La relation  est une relation d'ordre sur
est une relation d'ordre sur 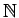 . Et ce que Sharkowski a démontré c'est que si une suite contient un
cycle d'ordre
. Et ce que Sharkowski a démontré c'est que si une suite contient un
cycle d'ordre  , alors
, alors
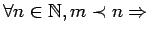 la suite contient une cycle d'ordre
la suite contient une cycle d'ordre  .
.
Un corollaire immédiat indique donc que si une suite possède un cycle d'ordre  , alors elle présente des cycles de tout ordre.
, alors elle présente des cycles de tout ordre.
De plus les cycles apparaîssent dans le sens inverse de la flèche, c'est à dire que l'on verra d'abord apparaître des cycles d'ordre 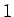 ,
puis d'ordre
,
puis d'ordre  , puis d'ordre
, puis d'ordre 

Lorsqu'il n'est plus possible d'atteindre une système stable, il est parfois possible d'obtenir des systèmes oscillants ou périodiques.
Dans ce cas même si on ne conserve pas un état constant, on passe cependant par des états parfaitements connus dans leur enchaînement et
dans leur constitution.
Ce sont donc des situations intéressantes dans le cas d'applications concrètes (comme un système mécanique) qui peuvent motiver la
recherche de cycles.
Cependant l'ensemble des cycles peut être diviser en deux :
- d'une part les cycles attractif (ou stables) : il s'agit d'un cycle limite vers lequel va tendre la suite pour presque toutes les
valeurs initiales,
- d'autre part les cycles répulsifs (ou instables) : même un point très proche d'une des valeurs du cycle finira par présenter un
comportement chaotique.
En fait, la différence entre un cycle stable et un cycle instable est semblable à celle qu'il existe entre un point fixe stable et un
point fixe instabble : le coefficient directeur de la tangente.
On remarquera que d'un point de vue physique, ou plus généralement dans le cas où l'on cherche à connaître l'état d'un système donnée à
longs termes, ce sont les cycles stables les plus intéressants.
Nous allons voir deux méthodes utilisées pour la recherche d'un  -cycle.
On cherche tout d'abord les points fixes de la fonction
-cycle.
On cherche tout d'abord les points fixes de la fonction  , c'est à dire les points d'intersections entre la courbe représentative de
, c'est à dire les points d'intersections entre la courbe représentative de
 et la droite d'équation
et la droite d'équation  .
.
Ensuite, on élimine les solutions qui correspondent à des cycles d'ordre inférieur.
Il nous reste alors  solutions qui correspondent aux valeurs que prend le cycle.
solutions qui correspondent aux valeurs que prend le cycle.
On doit trouver les racines d'un polynôme de degré  , MAPPLE nous renvoie les 8 valeurs réelles suivantes.
, MAPPLE nous renvoie les 8 valeurs réelles suivantes.
Il faut en suite vérifier que les valeurs appartiennent bien à un 4-cycle. Il reste alors les valeurs :
 .
.
Si on trace le graphique en prenant pour  l'une quelconque de ces valeurs, on obtient le graphe suivant.
l'une quelconque de ces valeurs, on obtient le graphe suivant.
Comme beaucoup de mot le chaos mathématique n'a pas le même sens que le chaos quotidien, voyons donc sa définition. Mais commençons par
introduire les termes sur lesquelles celle-ci s'appuie.
D'un point de vue mathématique on dit que  montre une dépendance sensible aux conditions initiales lorsque :
montre une dépendance sensible aux conditions initiales lorsque :
C'est ce que Lorenz à traduit par : "un battement d'aile de papillon au Brésil peut entraîner une tornade au Texas."
On dit que  est topologiquement transitive lorsque :
Une fonction est f définie sur une partie D d'un espace vectoriel normé est dite chaotique lorsque :
est topologiquement transitive lorsque :
Une fonction est f définie sur une partie D d'un espace vectoriel normé est dite chaotique lorsque :
- l'ensemble des points périodiques est dense dans D,
- f est topologiquement transitive (voir définition en annexe),
- f montre une dépendance sensible aux conditions initiales.
Pour  , la suite logistique répond à toutes ces conditions donc elle est chotique au sens mathématique du terme.
, la suite logistique répond à toutes ces conditions donc elle est chotique au sens mathématique du terme.
Nous allons ici présenter un exemple qui montre comment se manifeste l'effet papillon. Puis nous verrons quels problèmes il peut poser
dans les calculs scientifiques.
On va étudier à l'aide d'un exmple précis une manifestation de l'effet papillon.
On prend deux valeurs de  proches, par exemple
proches, par exemple  et
et  puis on étudie les comportements des deux suites ainsi
définies (en prenant bien soin d'effectuer les calculs avec une précision d'au moins 40 décimales). Pour cela, on va représenter
puis on étudie les comportements des deux suites ainsi
définies (en prenant bien soin d'effectuer les calculs avec une précision d'au moins 40 décimales). Pour cela, on va représenter  en
fonction de
en
fonction de  . Tant que les deux suites coïncideront, les points appartiendront à la première bissectrice du repère. C'est ce que l'on
constate sur la première figure.
. Tant que les deux suites coïncideront, les points appartiendront à la première bissectrice du repère. C'est ce que l'on
constate sur la première figure.
Mais dès que l'on augmente le nombre d'itérations, on obtient quelquechose de semblable à la figure suivante, ce qui montre
bien que les deux suites ont des comportements totalement différents.
La manifestation de l'effet papillon dans les calculs scientifiques apparaît de deux manières.
Tout d'abord, un système peut être imprédictible de par sa nature même, par exemple lorsqu'il est chaotique, comme c'est le cas pour la
suite logistique lorsque  .
.
Mais un autre facteur intervient. En effet, les ordinateurs effectuent leurs calculs en précision finie, ils introduisent donc une erreur
en troncant les décimales des nombres. Ce qui, comme nous l'avons vu, peut totalement fausser les résultats.
Nous allons illustrer ce phénomène avec un exemple simple.
On étudie toujours la suite logistique, avec le même système de représentation que précédemment, mais cette fois-ci on prend
 et
et
 et
et 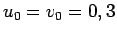 . D'un point de vue formel, les deux suites sont identiques, mais
prenons deux cas précis.
. D'un point de vue formel, les deux suites sont identiques, mais
prenons deux cas précis.
Dans un premier temps, on prend 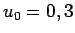 et on fait effectuer les calculs à MAPPLE avec une précision de
et on fait effectuer les calculs à MAPPLE avec une précision de 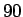 décimales sur
décimales sur  itérations. On obtient le graphique suivant :
itérations. On obtient le graphique suivant :
Il suffit cependant d'abaisser le nombre de décimales à  pour voir apparaître le graphique suivant :
pour voir apparaître le graphique suivant :
Ce qui traduit bien l'importance du nombre de décimales pour effectuer les calculs.
Encore une fois les deux suites ont un comportement différent. Mais cette fois-ci ce n'est pas du à un problème théorique,
mais à un problème pratique.
L'exemple précédent est important en météorologie, et plus généralement dans tous les domaines de la modélisations qui font appel à de
nombreux algorithmes récursifs.
Comme nous l'avons vu, pour effectuer des calculs valables à long terme, il faut donc effectuer les opérations avec un grand nombre de
décimales. Mais comme les modèles physiques s'appuient en plus sur un grand nombre de variables, il faut alors utiliser des calculateurs
surpuissants.
Ainsi, parmi les  plus puissants calculateurs mondiaux, on en retrouve
plus puissants calculateurs mondiaux, on en retrouve 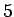 dédiés aux prévisions météorologiques, et
dédiés aux prévisions météorologiques, et  pour les
laboratoires de modélisation.
A travers de TIPE, nous avons mis en évidence le fait que même un système déterministe très simple peut être à l'origine de phénomènes
relativement complexes.
pour les
laboratoires de modélisation.
A travers de TIPE, nous avons mis en évidence le fait que même un système déterministe très simple peut être à l'origine de phénomènes
relativement complexes.
Ici, nous avons étudié la suite logistique qui semble être un cas isolé. Mais il existe tout un ensemble de systèmes qui présentent le même
comportement.
Il est donc intéressant de comprendre son fonctionnement pour pouvoir décrire des phénomènes plus compliqués.
En effet, aujourd'hui, on en retrouve des applications plus ou moins directe dans différents domaines :
| en physique |
: |
météorologie, |
| en biologie |
: |
étude des formes du vivant, |
| en sociologie |
: |
évolution des populations, |
| en économie |
: |
modélisation des fluctuations boursières, |
| en graphisme |
: |
fractales. |
Hasard et chaos, David Ruelle : Editions Odiles Jacob
Chaos et déterminisme, Dalmedico, Chabert, Chemla : Editions du Seuil
Dieu joue-t-il aux dés ?, Ian Stewart : Editions Flammarion
Science&Vie Junior : Les indispensables : Equations du second degré
Tangente : N° 64-65
Tangente : Hors-Série : Systèmes dynamiques
Toutes les procédures présentées ont été réalisées sous MAPPLE .
A chaque fois elles servent à étudier une suite de type :
Comme nous voulons étudier le comportement de la suite en fonction de  , on va essayer de représenter son comportement au voisinage
de l'infini en fonction de
, on va essayer de représenter son comportement au voisinage
de l'infini en fonction de  . On met donc en place un graphique à deux dimensions, où figureront en abscisses les valeurs de
. On met donc en place un graphique à deux dimensions, où figureront en abscisses les valeurs de  et en
ordonnées les valeurs de la suite au voisinage de l'infini.
et en
ordonnées les valeurs de la suite au voisinage de l'infini.
![$[Amin;Amax]$](img78.png) réprésente l'intervalle de variation de
réprésente l'intervalle de variation de  ,
,
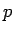 réprésente le pas utilisé,
réprésente le pas utilisé,
 correspond à la valeur de
correspond à la valeur de  à partir de laquelle on commence à afficher les points,
à partir de laquelle on commence à afficher les points,
 correspond à la valeur de
correspond à la valeur de  pour laquelle on stoppe les calculs.
pour laquelle on stoppe les calculs.
bifurc:=proc(Amin,Amax,p,Nmin,Nmax);
M:=NULL;
g:=x->(x*(1-x));
for a from Amin to Amax by p do
L:=NULL;
t:=0.4;
for k from 1 to Nmin do t:=a*evalf(g(t)) od;
for k from Nmin to Nmax do
L:=L,[a,t];
t:=evalf(a*g(t));
od;
M:=M,plot([L],x=Amin..Amax,style=point,symbol=point);
od;
display([M]);
end:
Il s'agit de réprésenter la fonction  qui définit la suite, ainsi que la droite d'équation
qui définit la suite, ainsi que la droite d'équation  , puis de montrer comment se définit
, puis de montrer comment se définit
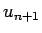 en fonction de
en fonction de  .
.
 est la fonction à partir de laquelle les calculs sont effectués,
est la fonction à partir de laquelle les calculs sont effectués,
 est le nombre d'itérations que l'on désire afficher,
est le nombre d'itérations que l'on désire afficher,
 est la valeur initiale de la suite.
est la valeur initiale de la suite.
suite:=proc(f,n,u0);
L:=[u0,0];
t:=u0;
for k from 1 to n do
L:=L,[t,t],[t,f(t)];
t:=f(t);
od;
plot([x,f(x),[L]],x=0..1,color=[black,red,blue]);
end:
On cherche ici à illustrer le phénomène de sensibilité aux conditions initiales. On prend donc deux suites ne différant que par leur terme
initial. Puis on représente les itérés de l'une en fonction des itérés de l'autre.
 : fonction qui définit les deux suites,
: fonction qui définit les deux suites,
 : terme initial de la première suite,
: terme initial de la première suite,
 : terme inital de la seconde suite,
: terme inital de la seconde suite,
 : nombre d'itérations à représenter.
: nombre d'itérations à représenter.
pap:=proc(f,u0,v0,n);
L:=[u0,v0];
x:=u0;
y:=v0;
for k from 1 to n do
x:=f(x);
y:=f(y);
L:=L,[x,y];
od;
plot([L],style=point);
end:
On utilise le même système de représentation que dans le cas précédent pour illustrer les erreurs d'arrondi que peut commettre
l'ordinateur. Ici le terme initial est le même pour les deux suites, mais c'est l'expression de  qui diffère, on prendra par exemple
qui diffère, on prendra par exemple  factorisée puis développée.
factorisée puis développée.
 et
et  : les fonctions définissant les deux suites,
: les fonctions définissant les deux suites,
 : le terme initial pour chaque suite,
: le terme initial pour chaque suite,
 : le nombre d'itérations à représenter.
: le nombre d'itérations à représenter.
pap2:=proc(f,g,u0,n);
L:=[u0,u0];
x:=u0;
y:=u0;
for k from 1 to n do
x:=f(x);
y:=g(y);
L:=L,[x,y];
od;
plot([L],style=point);
end:
L'effet papillon
This document was generated using the
LaTeX2HTML translator Version 2K.1beta (1.48)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html tipe4web.tex -split 0 -no_navigation
The translation was initiated by Sébastien Georget on 2003-09-18
Sébastien Georget
2003-09-18

![\begin{displaymath}
\left \{
\begin{array}{ccc}
u_0 &\in& [0;1]\\
u_{n+1} &=& f(u_n)
\end{array}
\right.
\end{displaymath}](img3.png)
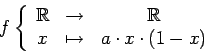
![\includegraphics[]{img/web_ex.ps}](img8.png)
![]() est déterminé à partir de
est déterminé à partir de ![]() , on trace la droite d'équation
, on trace la droite d'équation ![]() , puis à chaque itération, on reporte la
valeurde
, puis à chaque itération, on reporte la
valeurde ![]() sur cette droite et on en recherche l'image par
sur cette droite et on en recherche l'image par ![]() .
.
![]() accessible aux capacités de l'ordinateur. Ensuite nous représenterons les éléments de la suites pour
accessible aux capacités de l'ordinateur. Ensuite nous représenterons les éléments de la suites pour ![]() variant de
variant de ![]() à
à
![]() , en prenant
, en prenant ![]() suffisament grand pour qu'on soit quasiment sur du comportement de la suite, mais pas trop grand afin de conservé
des temps de calcul raisonnables.
suffisament grand pour qu'on soit quasiment sur du comportement de la suite, mais pas trop grand afin de conservé
des temps de calcul raisonnables.
![[*]](crossref.png) ), le diagramme de bifurcation suivant, aussi appelé
diagramme de FeigenBaum.
), le diagramme de bifurcation suivant, aussi appelé
diagramme de FeigenBaum.
![\includegraphics[]{img/bifurc0.ps}](img19.png)
![]() à partir desquelles le diagramme se divise en deux. Ce qui se traduit au
niveau de la suite par l'apparition de cycles.
à partir desquelles le diagramme se divise en deux. Ce qui se traduit au
niveau de la suite par l'apparition de cycles.
![\includegraphics[]{img/web25.ps}](img23.png)
![\includegraphics[]{img/web25z.ps}](img24.png)
![\includegraphics[]{img/web32.ps}](img25.png)
![\includegraphics[]{img/web32z.ps}](img26.png)
![]() bifurcation, il faut résoudre l'équation
bifurcation, il faut résoudre l'équation ![]() , c'est à dire un polynôme de degré
, c'est à dire un polynôme de degré ![]() . On
n'obtiendra donc que des valeurs approchées.
. On
n'obtiendra donc que des valeurs approchées.
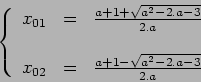
![\begin{displaymath}
\left \{
\begin{array}{ccc}
f^p(x) &\neq x,& $ si p$\ ...
...1] \\
f^p(x) &= x,& $ si $\ n = p
\end{array}
\right.
\end{displaymath}](img37.png)
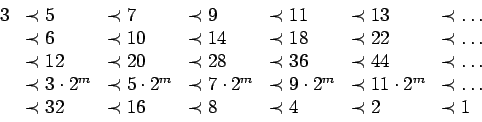
![\includegraphics[]{img/f4.ps}](img50.png)
![\includegraphics[]{img/f1234.ps}](img51.png)

![\includegraphics[]{img/cycle4.ps}](img56.png)

![]() , la suite logistique répond à toutes ces conditions donc elle est chotique au sens mathématique du terme.
, la suite logistique répond à toutes ces conditions donc elle est chotique au sens mathématique du terme.
![\includegraphics[]{img/pap1.ps}](img63.png)
![\includegraphics[]{img/pap2.ps}](img64.png)
![]() et
et
![]() et
et ![]() . D'un point de vue formel, les deux suites sont identiques, mais
prenons deux cas précis.
. D'un point de vue formel, les deux suites sont identiques, mais
prenons deux cas précis.
![]() et on fait effectuer les calculs à MAPPLE avec une précision de
et on fait effectuer les calculs à MAPPLE avec une précision de ![]() décimales sur
décimales sur ![]() itérations. On obtient le graphique suivant :
itérations. On obtient le graphique suivant :
![\includegraphics[]{img/papfg1.ps}](img72.png)
![\includegraphics[]{img/papfg2.ps}](img74.png)
![\begin{displaymath}
\left \{
\begin{array}{ccc}
u_0 &\in& [0;1]\\
u_{n+1} &=& f(u_n)
\end{array}
\right.
\end{displaymath}](img3.png)