



suivant: Conclusion
monter: L'effet papillon
précédent: On tourne en rond
Table des matières
Sous-sections
Comme beaucoup de mot le chaos mathématique n'a pas le même sens que le chaos quotidien, voyons donc sa définition. Mais commençons par
introduire les termes sur lesquelles celle-ci s'appuie.
D'un point de vue mathématique on dit que  montre une dépendance sensible aux conditions initiales lorsque :
montre une dépendance sensible aux conditions initiales lorsque :
C'est ce que Lorenz à traduit par : "un battement d'aile de papillon au Brésil peut entraîner une tornade au Texas."
On dit que  est topologiquement transitive lorsque :
Une fonction est f définie sur une partie D d'un espace vectoriel normé est dite chaotique lorsque :
est topologiquement transitive lorsque :
Une fonction est f définie sur une partie D d'un espace vectoriel normé est dite chaotique lorsque :
- l'ensemble des points périodiques est dense dans D,
- f est topologiquement transitive (voir définition en annexe),
- f montre une dépendance sensible aux conditions initiales.
Pour  , la suite logistique répond à toutes ces conditions donc elle est chotique au sens mathématique du terme.
, la suite logistique répond à toutes ces conditions donc elle est chotique au sens mathématique du terme.
Nous allons ici présenter un exemple qui montre comment se manifeste l'effet papillon. Puis nous verrons quels problèmes il peut poser
dans les calculs scientifiques.
On va étudier à l'aide d'un exmple précis une manifestation de l'effet papillon.
On prend deux valeurs de  proches, par exemple
proches, par exemple  et
et  puis on étudie les comportements des deux suites ainsi
définies (en prenant bien soin d'effectuer les calculs avec une précision d'au moins 40 décimales). Pour cela, on va représenter
puis on étudie les comportements des deux suites ainsi
définies (en prenant bien soin d'effectuer les calculs avec une précision d'au moins 40 décimales). Pour cela, on va représenter  en
fonction de
en
fonction de  . Tant que les deux suites coïncideront, les points appartiendront à la première bissectrice du repère. C'est ce que l'on
constate sur la première figure.
. Tant que les deux suites coïncideront, les points appartiendront à la première bissectrice du repère. C'est ce que l'on
constate sur la première figure.
Mais dès que l'on augmente le nombre d'itérations, on obtient quelquechose de semblable à la figure suivante, ce qui montre
bien que les deux suites ont des comportements totalement différents.
La manifestation de l'effet papillon dans les calculs scientifiques apparaît de deux manières.
Tout d'abord, un système peut être imprédictible de par sa nature même, par exemple lorsqu'il est chaotique, comme c'est le cas pour la
suite logistique lorsque  .
.
Mais un autre facteur intervient. En effet, les ordinateurs effectuent leurs calculs en précision finie, ils introduisent donc une erreur
en troncant les décimales des nombres. Ce qui, comme nous l'avons vu, peut totalement fausser les résultats.
Nous allons illustrer ce phénomène avec un exemple simple.
On étudie toujours la suite logistique, avec le même système de représentation que précédemment, mais cette fois-ci on prend
 et
et
 et
et 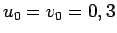 . D'un point de vue formel, les deux suites sont identiques, mais
prenons deux cas précis.
. D'un point de vue formel, les deux suites sont identiques, mais
prenons deux cas précis.
Dans un premier temps, on prend 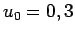 et on fait effectuer les calculs à MAPPLE avec une précision de
et on fait effectuer les calculs à MAPPLE avec une précision de 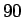 décimales sur
décimales sur  itérations. On obtient le graphique suivant :
itérations. On obtient le graphique suivant :
Il suffit cependant d'abaisser le nombre de décimales à  pour voir apparaître le graphique suivant :
pour voir apparaître le graphique suivant :
Ce qui traduit bien l'importance du nombre de décimales pour effectuer les calculs.
Encore une fois les deux suites ont un comportement différent. Mais cette fois-ci ce n'est pas du à un problème théorique,
mais à un problème pratique.
L'exemple précédent est important en météorologie, et plus généralement dans tous les domaines de la modélisations qui font appel à de
nombreux algorithmes récursifs.
Comme nous l'avons vu, pour effectuer des calculs valables à long terme, il faut donc effectuer les opérations avec un grand nombre de
décimales. Mais comme les modèles physiques s'appuient en plus sur un grand nombre de variables, il faut alors utiliser des calculateurs
surpuissants.
Ainsi, parmi les  plus puissants calculateurs mondiaux, on en retrouve
plus puissants calculateurs mondiaux, on en retrouve 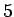 dédiés aux prévisions météorologiques, et
dédiés aux prévisions météorologiques, et  pour les
laboratoires de modélisation.
pour les
laboratoires de modélisation.




suivant: Conclusion
monter: L'effet papillon
précédent: On tourne en rond
Table des matières
Sébastien Georget
2003-09-18


![]() , la suite logistique répond à toutes ces conditions donc elle est chotique au sens mathématique du terme.
, la suite logistique répond à toutes ces conditions donc elle est chotique au sens mathématique du terme.
![\includegraphics[]{img/pap1.ps}](img63.png)
![\includegraphics[]{img/pap2.ps}](img64.png)
![]() et
et
![]() et
et ![]() . D'un point de vue formel, les deux suites sont identiques, mais
prenons deux cas précis.
. D'un point de vue formel, les deux suites sont identiques, mais
prenons deux cas précis.
![]() et on fait effectuer les calculs à MAPPLE avec une précision de
et on fait effectuer les calculs à MAPPLE avec une précision de ![]() décimales sur
décimales sur ![]() itérations. On obtient le graphique suivant :
itérations. On obtient le graphique suivant :
![\includegraphics[]{img/papfg1.ps}](img72.png)
![\includegraphics[]{img/papfg2.ps}](img74.png)