



suivant: Le chaos
monter: L'effet papillon
précédent: Premiers pas
Table des matières
Sous-sections
Nous allons commencer par définir mathématiquement un cycle, puis nous verrons un théorème important pour l'étude de la suite logistique.
On définit un n-cycle ou cycle d'ordre n de la manière suivant :
avec :
A partir du diagramme de Feigenbaum, on peut penser que les cycles vont apparaîtres dans l'ordre des puissances de  .
.
C'est effectivement le cas, mais grâce à un mathématicien russe : A.N. Sharkovski, on sait depuis 1964 que ce ne sont pas les
seuls. Il a même démontré dans quels ordre apparaîssent les cycles. C'est ce que nous allons voir maintenant.
La relation 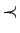 est une relation d'ordre sur
est une relation d'ordre sur 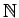 . Et ce que Sharkowski a démontré c'est que si une suite contient un
cycle d'ordre
. Et ce que Sharkowski a démontré c'est que si une suite contient un
cycle d'ordre  , alors
, alors
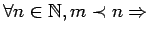 la suite contient une cycle d'ordre
la suite contient une cycle d'ordre  .
.
Un corollaire immédiat indique donc que si une suite possède un cycle d'ordre  , alors elle présente des cycles de tout ordre.
, alors elle présente des cycles de tout ordre.
De plus les cycles apparaîssent dans le sens inverse de la flèche, c'est à dire que l'on verra d'abord apparaître des cycles d'ordre 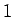 ,
puis d'ordre
,
puis d'ordre  , puis d'ordre
, puis d'ordre 

Lorsqu'il n'est plus possible d'atteindre une système stable, il est parfois possible d'obtenir des systèmes oscillants ou périodiques.
Dans ce cas même si on ne conserve pas un état constant, on passe cependant par des états parfaitements connus dans leur enchaînement et
dans leur constitution.
Ce sont donc des situations intéressantes dans le cas d'applications concrètes (comme un système mécanique) qui peuvent motiver la
recherche de cycles.
Cependant l'ensemble des cycles peut être diviser en deux :
- d'une part les cycles attractif (ou stables) : il s'agit d'un cycle limite vers lequel va tendre la suite pour presque toutes les
valeurs initiales,
- d'autre part les cycles répulsifs (ou instables) : même un point très proche d'une des valeurs du cycle finira par présenter un
comportement chaotique.
En fait, la différence entre un cycle stable et un cycle instable est semblable à celle qu'il existe entre un point fixe stable et un
point fixe instabble : le coefficient directeur de la tangente.
On remarquera que d'un point de vue physique, ou plus généralement dans le cas où l'on cherche à connaître l'état d'un système donnée à
longs termes, ce sont les cycles stables les plus intéressants.
Nous allons voir deux méthodes utilisées pour la recherche d'un  -cycle.
On cherche tout d'abord les points fixes de la fonction
-cycle.
On cherche tout d'abord les points fixes de la fonction 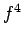 , c'est à dire les points d'intersections entre la courbe représentative de
, c'est à dire les points d'intersections entre la courbe représentative de
 et la droite d'équation
et la droite d'équation  .
.
Ensuite, on élimine les solutions qui correspondent à des cycles d'ordre inférieur.
Il nous reste alors  solutions qui correspondent aux valeurs que prend le cycle.
solutions qui correspondent aux valeurs que prend le cycle.
On doit trouver les racines d'un polynôme de degré  , MAPPLE nous renvoie les 8 valeurs réelles suivantes.
, MAPPLE nous renvoie les 8 valeurs réelles suivantes.
Il faut en suite vérifier que les valeurs appartiennent bien à un 4-cycle. Il reste alors les valeurs :
 .
.
Si on trace le graphique en prenant pour  l'une quelconque de ces valeurs, on obtient le graphe suivant.
l'une quelconque de ces valeurs, on obtient le graphe suivant.




suivant: Le chaos
monter: L'effet papillon
précédent: Premiers pas
Table des matières
Sébastien Georget
2003-09-18
![\begin{displaymath}
\left \{
\begin{array}{ccc}
f^p(x) &\neq x,& $ si p$\ ...
...1] \\
f^p(x) &= x,& $ si $\ n = p
\end{array}
\right.
\end{displaymath}](img37.png)
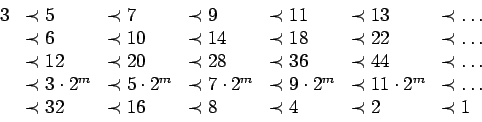
![\includegraphics[]{img/f4.ps}](img50.png)
![\includegraphics[]{img/f1234.ps}](img51.png)

![\includegraphics[]{img/cycle4.ps}](img56.png)