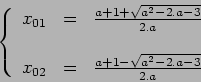suivant: On tourne en rond
monter: L'effet papillon
précédent: Présentation
Table des matières
Sous-sections
Dans cette section, nous allons définir ce qu'est la suite logistique puis nous verrons une méthode pratique permettant de la construire et
de l'étudier.
La suite logistique est définie ainsi :
où la fonction  est une fonction paramétrée définie de la manière suivante :
est une fonction paramétrée définie de la manière suivante :
On prendra par la suite ![$a \in [0;4]$](img6.png) de manière à ce que l'intervalle
de manière à ce que l'intervalle ![$[0;1]$](img7.png) soit stable par
soit stable par  .
.
Pour visualiser une telle suite il existe une représentation utile que l'on appelle la représentation en toile d'araignée. Nous allons
voir avec un exemple comment elle fonctionne.
Puisque 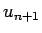 est déterminé à partir de
est déterminé à partir de  , on trace la droite d'équation
, on trace la droite d'équation  , puis à chaque itération, on reporte la
valeurde
, puis à chaque itération, on reporte la
valeurde  sur cette droite et on en recherche l'image par
sur cette droite et on en recherche l'image par  .
.
Sur l'exemple précédent, nous avons vu que la suite convergeait vers un point fixe. On peut se demander si se comportement est valable
pour toutes les valeurs de ![$a \in [0;4]$](img6.png) . Pour voir rapidement ce qu'il en est nous allons utiliser le diagramme de bifurcation.
. Pour voir rapidement ce qu'il en est nous allons utiliser le diagramme de bifurcation.
Comme nous voulons étudier le comportement de la suite en fonction de  , on va essayer de représenter son comportement au voisinage
de l'infini en fonction de
, on va essayer de représenter son comportement au voisinage
de l'infini en fonction de  . On met donc en place un graphique à deux dimensions, où figureront en abscisses les valeurs de
. On met donc en place un graphique à deux dimensions, où figureront en abscisses les valeurs de  et en
ordonnées les valeurs de la suite au voisinage de l'infini.
et en
ordonnées les valeurs de la suite au voisinage de l'infini.
On supposera en fait que le comportement de la suite se stabilise très vite. Ce qui nous permettra d'étudier la suite à partir d'un
rang  accessible aux capacités de l'ordinateur. Ensuite nous représenterons les éléments de la suites pour
accessible aux capacités de l'ordinateur. Ensuite nous représenterons les éléments de la suites pour  variant de
variant de  à
à
 , en prenant
, en prenant  suffisament grand pour qu'on soit quasiment sur du comportement de la suite, mais pas trop grand afin de conservé
des temps de calcul raisonnables.
suffisament grand pour qu'on soit quasiment sur du comportement de la suite, mais pas trop grand afin de conservé
des temps de calcul raisonnables.
Ici, nous avons choisi  et
et  .
.
Nous obtenons grâce à la procédure bifurc (voir page ![[*]](crossref.png) ), le diagramme de bifurcation suivant, aussi appelé
diagramme de FeigenBaum.
), le diagramme de bifurcation suivant, aussi appelé
diagramme de FeigenBaum.
On peut tout de suite voir que la suite ne présente pas toujours un comportement aussi simple que celui que nous avons vu
précédemment. En effet, il semble qu'il existe des valeurs de  à partir desquelles le diagramme se divise en deux. Ce qui se traduit au
niveau de la suite par l'apparition de cycles.
à partir desquelles le diagramme se divise en deux. Ce qui se traduit au
niveau de la suite par l'apparition de cycles.
Tout d'abord, nous allons nous limiter à l'étude de la première bifurcation. C'est à dire que nous allons chercher pour quelle valeur
de  la suite ne converge plus. Mais pour cela, nous devons essayer de comprendre pourquoi la convergence disparaît, c'est ce que nous
allons voir.
la suite ne converge plus. Mais pour cela, nous devons essayer de comprendre pourquoi la convergence disparaît, c'est ce que nous
allons voir.
En fait, la représentation en toile d'araignée va nous permettre de comprendre ce qui se passe.
Etudions localement comment se comporte la suite dans le domaine de convergence (par exemple  ) et dans le domaine où
elle ne converge plus (par exemple
) et dans le domaine où
elle ne converge plus (par exemple  ).
Rerprésentons en plus sur les schémas la tangente au point d'intersection
).
Rerprésentons en plus sur les schémas la tangente au point d'intersection  entre la courbe représentative de
entre la courbe représentative de  et la première
bissectrice du repère.
et la première
bissectrice du repère.
Graphiquement, on comprend bien pourquoi la suite va cesser de converger.
En effet, tant que le coefficient directeur de la tangente en  est supérieur à
est supérieur à  , localement chaque itéré se rapproche du point
fixe. Dans ce cas, le point fixe est un point attractif (ou stable). Mais dès qu'il est inférieur à
, localement chaque itéré se rapproche du point
fixe. Dans ce cas, le point fixe est un point attractif (ou stable). Mais dès qu'il est inférieur à  , les itérés auront tendance à s'en
écarter. On dit alors que le point devient répulsif (ou instable).
, les itérés auront tendance à s'en
écarter. On dit alors que le point devient répulsif (ou instable).
Pour trouver la valeur de  à partir de laquelle la suite ne converge plus,
il faut donc trouver quand le coefficient de la tangente au point fixe passe par
à partir de laquelle la suite ne converge plus,
il faut donc trouver quand le coefficient de la tangente au point fixe passe par  .
.
Nous devons donc, dans un premier temps, résoudre l'équation  afin de déterminer le point fixe. On obient
afin de déterminer le point fixe. On obient
 .
.
Il nous faut ensuite déterminer la dérivée en ce point : 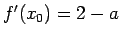 .
.
On trouve donc que la suite cesse de converger lorsque  , ce qu'on pouvait deviner sur le graphique.
, ce qu'on pouvait deviner sur le graphique.
On pourrait poursuive et déterminer ainsi les points de bifurcation suivants. Cependant les calculs deviennent rapidement très lourds,
puisque pour déterminer le point de 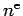 bifurcation, il faut résoudre l'équation
bifurcation, il faut résoudre l'équation  , c'est à dire un polynôme de degré
, c'est à dire un polynôme de degré  . On
n'obtiendra donc que des valeurs approchées.
. On
n'obtiendra donc que des valeurs approchées.
A titre d'exemple voici les deux points de bifurcation suivants.
Cet exemple, laisse supposer que pour chaque nouvelle branche définie, la bifurcation suivante aura lieu en même temps que sur les
autres branches.




suivant: On tourne en rond
monter: L'effet papillon
précédent: Présentation
Table des matières
Sébastien Georget
2003-09-18
![\begin{displaymath}
\left \{
\begin{array}{ccc}
u_0 &\in& [0;1]\\
u_{n+1} &=& f(u_n)
\end{array}
\right.
\end{displaymath}](img3.png)
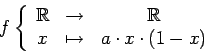
![\includegraphics[]{img/web_ex.ps}](img8.png)
![]() est déterminé à partir de
est déterminé à partir de ![]() , on trace la droite d'équation
, on trace la droite d'équation ![]() , puis à chaque itération, on reporte la
valeurde
, puis à chaque itération, on reporte la
valeurde ![]() sur cette droite et on en recherche l'image par
sur cette droite et on en recherche l'image par ![]() .
.
![]() accessible aux capacités de l'ordinateur. Ensuite nous représenterons les éléments de la suites pour
accessible aux capacités de l'ordinateur. Ensuite nous représenterons les éléments de la suites pour ![]() variant de
variant de ![]() à
à
![]() , en prenant
, en prenant ![]() suffisament grand pour qu'on soit quasiment sur du comportement de la suite, mais pas trop grand afin de conservé
des temps de calcul raisonnables.
suffisament grand pour qu'on soit quasiment sur du comportement de la suite, mais pas trop grand afin de conservé
des temps de calcul raisonnables.
![[*]](crossref.png) ), le diagramme de bifurcation suivant, aussi appelé
diagramme de FeigenBaum.
), le diagramme de bifurcation suivant, aussi appelé
diagramme de FeigenBaum.
![\includegraphics[]{img/bifurc0.ps}](img19.png)
![]() à partir desquelles le diagramme se divise en deux. Ce qui se traduit au
niveau de la suite par l'apparition de cycles.
à partir desquelles le diagramme se divise en deux. Ce qui se traduit au
niveau de la suite par l'apparition de cycles.
![\includegraphics[]{img/web25.ps}](img23.png)
![\includegraphics[]{img/web25z.ps}](img24.png)
![\includegraphics[]{img/web32.ps}](img25.png)
![\includegraphics[]{img/web32z.ps}](img26.png)
![]() bifurcation, il faut résoudre l'équation
bifurcation, il faut résoudre l'équation ![]() , c'est à dire un polynôme de degré
, c'est à dire un polynôme de degré ![]() . On
n'obtiendra donc que des valeurs approchées.
. On
n'obtiendra donc que des valeurs approchées.